离散数学基础

进制与进制转换

进制

一般我们在生活中会使用十进制来表示数字，也就是逢十进一，但是在计算机的世界里，由于物理特性，我们使用二进制来存储和计算数据。

而我们所说的 $k$ 进制，也就是一个数每一位上由 $0,1,2,⋯,k−1$ 构成的数字。常见和常考的进制有二、八、十、十六进制四种。

其中十六进制一般用 $a,b,c,d,e,f$ 表示十进制中的 $10,11,12,13,14,15$。

十进制转 k 进制

我们一般使用短除法来实现任意进制的转换，若要将 $a$ 进制的 $s$ 转换为 $b$ 进制，将 $s$ 每次除以 $b$，得到的余数的逆序列是 $b$ 进制表示的结果。每次除的时候用到同余模定理，即从最高位开始除，得到的余数乘以 $a$ 加到下一位，一直到最低位。

而十进制由于余数乘 $10$ 在正常的进制表示中看就是将数字的右边添加一个 $0$，可以用更简单的表示。

例如将十进制的 $52$ 转换为二进制：

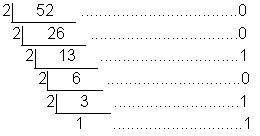
每次用当前的数除以 $2$，得出商和余数，将商写在下方，余数写在右方。最后将右方的所有余数倒序排列就是二进制表示。

k 进制转十进制

将 $k$ 进制转换为十进制有更简单的方法。例如，对于 $(100101)_2$，我们可以用如下的方式进行进制转换：

$$(100101)_2=1×2^5+0×2^4+0×2^3+1×2^2+0×2^1+1×2^0=37$$

本质上就是算出每个 $X$ 进制位上的值实际上是多少，累加得出最终的结果。

2、8、16 进制的互相转换

对于这三种进制有更简单的转换方法，比如 $(10110)_2$ 转八进制，首先按 $3$ 位补齐，变成 $(010,110)_2$。

然后每三位合并出一个 8 进制数变成 $(26)_8$ 即可。

而八进制转二进制、八转十六、十六转八也都是同理，按三位隔开即可。

二进制转十六进制则是 $4$ 位变 $1$ 位，下面给出转换表格：

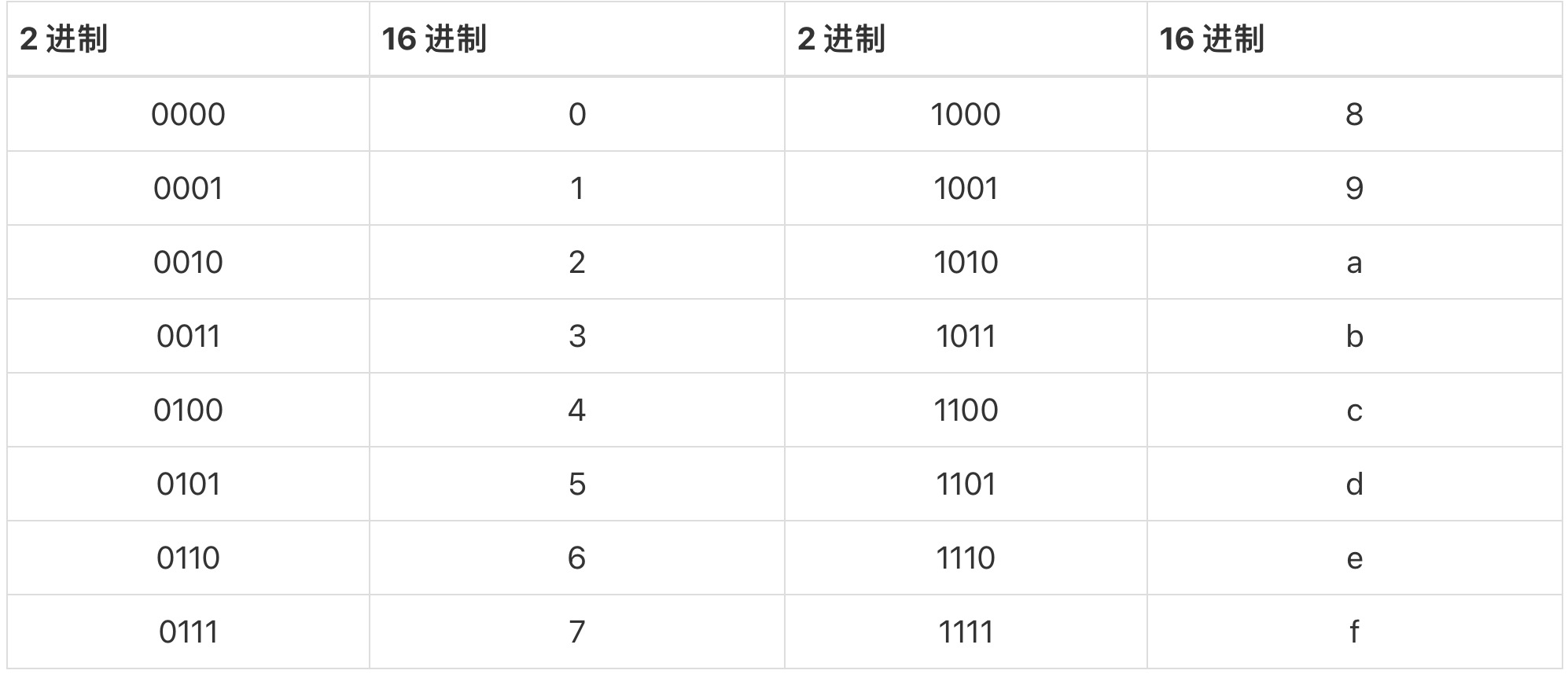
也是补齐到 $4$ 位，然后直接转换即可。

二进制的位运算

• &：按位与

• |：按位或

• ^：按位异或

• ~：按位取反

• <<：左移

• >>：右移

需要理解并能准确算出这些位运算符的计算结果。

浮点数的进制转换

$k$ 进制浮点数的处理相对而言算是一个难点，关键在于如何理解不在十进制下的小数表示。

例如，对于二进制小数 $(10.101)_2$ 来说，我们可以通过如下的方法把它转换成十进制小数：

$$\begin{aligned} (10.101)2 =& 1 \times 2 ^ 1 + 0 \times 2 ^ 0 + 1 \times 2 ^ {-1} + 0 \times 2 ^ {-2} + 1 \times 2 ^ {-3} \cr=& 2 + 0.5 + 0.125 \cr=& (2.625){10} \end{aligned}$$

而其实有的十进制小数无法转换为二进制小数，而且转换起来比较复杂，所以一般不会考察。

还有一类考察 $2,8,16$ 进制的小数之间的互相转换。类似于整数的互相转换，补齐位数后来做。

10.11

以小数点为基准点，从小数点向前每三个分为一组，从小数点向后每三个分为一组，不足的补零：

010.110

之后，将每组二进制数转换为八进制数：

2.6

因此，$(10.11)_2 = (2.6)_8$。

数值编码

通常考察的知识点如下：

• 原码、反码、补码的定义与计算

• 浮点数的编码

• ASCII 码的计算

ASCII 码

主要记住 $'0'=48$，$'A'=65$，$'a' = 97$ 即可。

原码、反码和补码

在计算机中，所有数据都是以二进制的形式存储的。那么我们如何用二进制表示负数呢？就需要学习原码、反码和补码。

无论原码、反码还是补码，第一位都是符号位，当第一位为 $0$ 时，表示正数；反之表示负数。

原码：除符号位外，余下位上的数为原数的绝对值。

反码：正数的反码就是其本身；负数的反码是在原码的基础之上，符号位不变，余下的所有位取反。

补码：正数的补码就是其本身；负数的补码就是在反码的基础之上 $+1$。

我们通过如下几个例子来进一步理解原码、反码和补码：

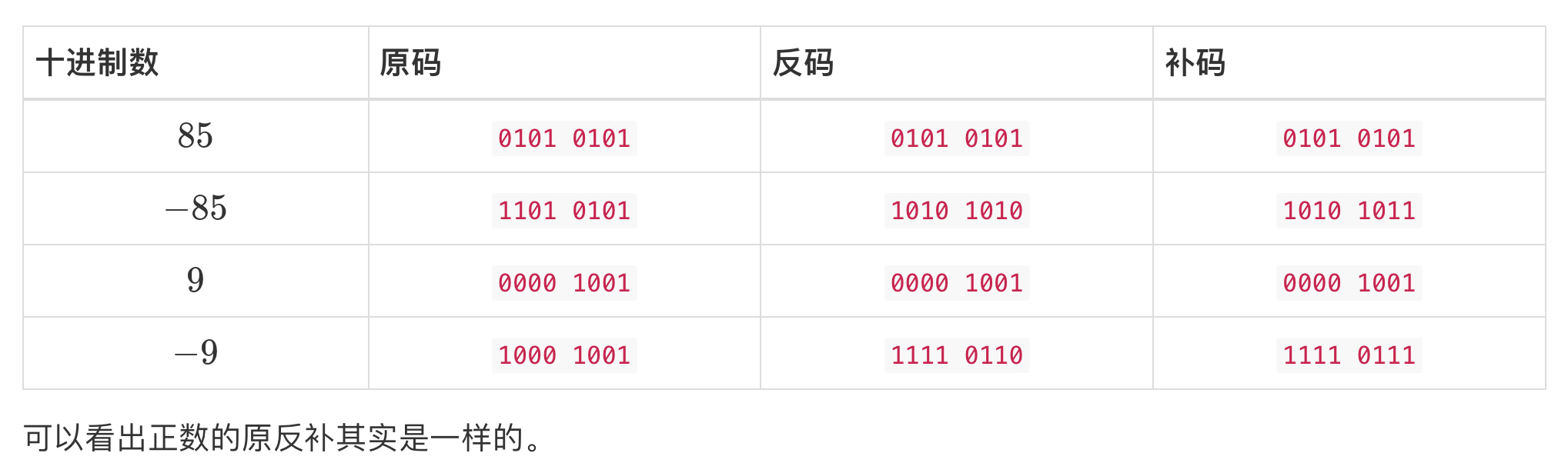
浮点数编码

在计算机中存储的小数之所以被称为“浮点数”，与它的存储方式是分不开的。目前通用的存储方式为 IEEE 二进制浮点数算术标准（IEEE 754），浮点数由三部分组成：

符号（$sign$）：负数为 $1$，正数为 $0$

尾数（$exponent$）：一个二进制小数

阶码（$significand$）：表示 $2$ 的多少次幂

浮点数的值就是 ${sign}significand × 2 ^ {exponent}$ ，因为用类似科学计数法的方式存储小数，所以我们往往对计算机存储的小数称为浮点数，也就是“浮动小数点的数”。

对于float类型（32 位浮点数）而言，符号位 $1$ 位、尾数 $23$ 位、阶码 $8$ 位。对于double类型（64 位浮点数）而言，符号位 $1$ 位、尾数 $52$ 位，阶码 $11$ 位。

float的尾数有 $2^{23}=8388608$ 种，也就意味着float最多能有 $7$ 位有效数字；double的尾数有 $2^{52}=4503599627370496$，也就意味着double的精度有 $15-16$ 位。

在double转float的过程中，尾数部分和阶码部分会分开进行强制转换，丢弃多出来的部分。

而且这样储存尾数就会导致运算过程中会出现精度误差，比如一个无限小数我们实际上储存的是它的前某些位，他们做加减乘除都是可能产生误差的。而且是一个误差逐渐提高的过程，因为在某一步出现误差之后丢弃的部分是不能返还的。

还有一点是浮点数在做等于的比较时，我们需要去使用一个 eps 误差量，在 $a$ 和 $b$ 的差的绝对值不超过 eps 时我们就认为两者相等，直接使用 == 去判断时会比较他们二进制表示中的每一位导致误差，甚至在强制转换的过程中导致不等的返回等于的结果。

逻辑运算

他们之间的优先级按照“非 > 与 > 或”排列，同级运算符从左向右依次计算。

而且在 C/C++ 中逻辑运算是有短路性的，也就是说同级运算中先计算出来的东西如果满足条件就不会往下继续计算了，例如：

int a = 1;
int b = 1;
if (a || ++b) {
  ...
}

此时 b 仍然是 $1$。