线段树

引入

为了解决问题，我们介绍一种灵活的数据结构——线段树。

简介

我们用一棵二叉树来表示线段树，线段树中的每个结点都表示一个区间。每个非叶子结点都有左右两棵子树，分别对应区间的 "左半" 和 "右半"。为了方便起见，我们给根结点编号为 $1$。对于每个结点，其左结点的编号为 $2i$，其右结点的编号为 $2i+1$。

对于一个结点，如果其表示的区间为 $[l,r]$。分情况如果 $l=r$，那么这个是一个叶子结点。否则令 $mid=⌊2l+r⌋$，左儿子对应的区间为 $[l,mid]$，右儿子对应的区间为 $[mid+1,r]$，这一思想有点类似二分。下面就是 $n=10$ 的时候的线段树。

解题

建树

前面构建的线段树，只是展示了线段树中各结点所对应的区间，但是对于用到线段树的大部分题目来说，这些线段所拥有的附加信息才是重头戏。比如要维护区间最小值问题，我们用一个额外的数组 $minv$ 记录每个结点对应的区间的最小值。

对于叶子结点，最小值就是一个数。而对于非叶子结点，区间的最小值就是左儿子的最小值和右儿子最小值中的最小值。

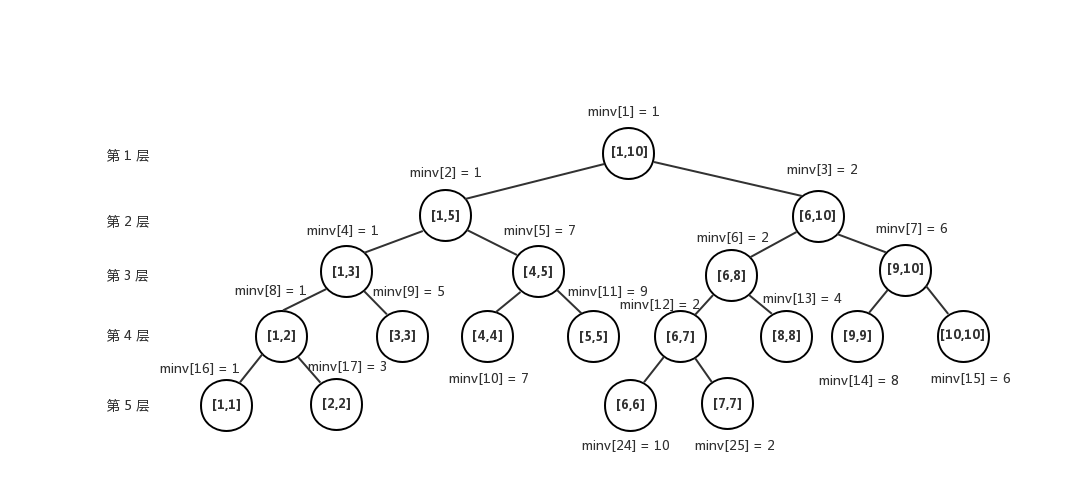
可以发现这个构建过程是一个递归的过程，父节点的信息需要用子节点去更新，所以我们需要先递归的构建好左右子树。见下面代码。

const int maxn = 10010;
int minv[4 * maxn], a[maxn]; // id 表示结点编号，l, r 表示左右区间
void build(int id, int l, int r) {
    if (l == r) {
        minv[id] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(id << 1, l, mid);
    build(id << 1 | 1, mid + 1, r);
    minv[id] = min(minv[id << 1], minv[id << 1 | 1]);
}

有一个需要特别注意的地方地方，虽然线段树中总的结点数是区间长度的两倍，但是实际上，我们结点的编号不一定是连续的，所以需要开更多的内存。而 $4$ 倍这个数字可以通过比较复杂的数学推导得出来。这里不做过多的推导了。

所以，整个建树的过程，时间复杂度是 $O(n)$。

修改

接着我们看如何进行单点更新（区间操作见后续博客）。如果是把整棵树推倒了全部重建，那未免也太不划算了。仔细分析，一个点的修改，只会影响到包含这个点的区间，而包含这个点的区间在树上实际上是一条链，比如我们更新 $ a_6 = 1 $，那么我们更新的方式如下: 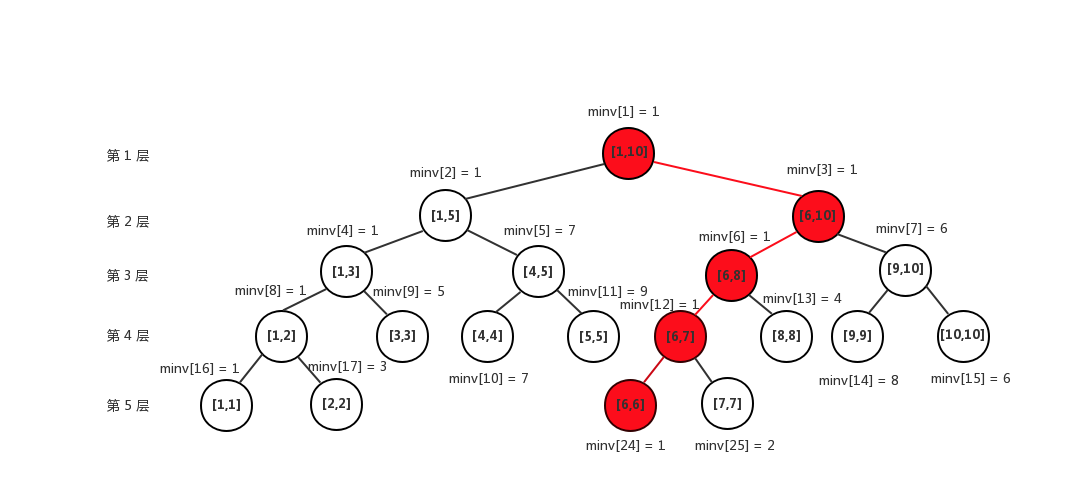一般，我们我们可以认为线段树的最大深度为 $\log n$，所以这条链的最大长度也是 $\log n$，所以一次更新时间复杂度是 $O(\log n)$ 。

对应的代码其实就很简单了:

// 把 x 位置更为成为 v
void update(int id, int l, int r, int x, int v) {
    if (l == r) {
        minv[id] = v;
        return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid) {
        update(id << 1, l, mid, x, v);
    } else {
        update(id << 1 | 1, mid + 1, r, x, v);
    }
    pushup(id);
}

查询

线段树的查询分成单点查询和区间查询。

单点查询

单点查询其实很简单，和单点更新一样，一直沿着链走到叶子结点就可以了。

int query(int id, int l, int r, int x) {
    if (l == r) {
        return minv[id];
    }
    int mid = (l + r) >> 1;
    if (mid <= x) {
        return query(id << 1, l, mid, x);
    } else {
        return query(id << 1 | 1, mid + 1, r, x);
    }
}

区间查询

单点查询其实是区间查询的特殊情况。

对于查询的区间 $[x,y]$ 我们可以划分为线段树上的结点，这些结点的区间合并起来就可以得到所需信息。

比如查询区间 $[3,6]$ 就是由下面这些红点合并起来的，其中绿点表示与被查询的区间 $[x,y]$ 有交集的结点。 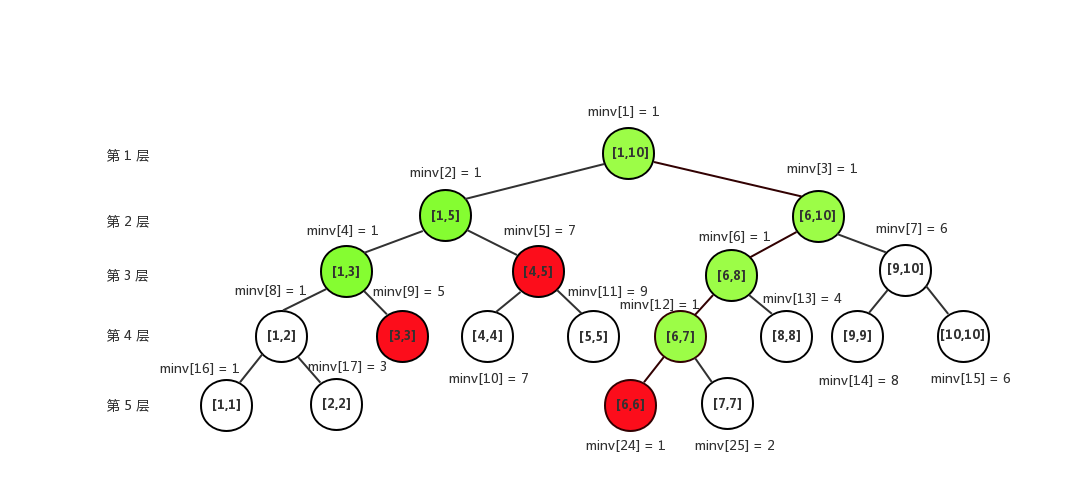我们发现，查询到一个红色的结点，可以直接返回，因为此时，区间 $[x,y]$ 是完全覆盖红点所在的区间的，而一个绿色的结点我们还需要继续递归，不过我们可以发现，每一层最多只会有两个绿点，最左边一个和最右边一个，这两个绿点中间的点都能被区间 $[x,y]$ 完全覆盖，所以最多只会有 $2\log n$ 个绿点，所以一次区间查询的复杂度也是 $\log n$。

int query(int id, int l, int r, int x, int y) {
    if (x <= l && r <= y) {  // 如果完全包含，直接返回
        return minv[id];
    }
    int mid = (l + r) >> 1;
    int ans = inf;
    if (x <= mid) {
        ans = min(ans, query(id << 1, l, mid, x, y));  // 如果左区间包含，递归的查询左子树
    }
    if (y > mid) {
        ans = min(ans, query(id << 1 | 1, mid + 1, r, x, y));  // 如果右区间包含，递归的查询右子树
    }
    return ans;
}